最近在看 Andrew Ng 老师的 机器学习课程 ，这篇文章试图通过编程的方式，一步步实验课程中的知识点，验证其中的一些结论，从而加深对逻辑回归的理解。

全文代码在 lotabout/logistic-regression-experiment.py

Sigmoid 函数的作用

在课程的引言里，给了一个二分类的任务，根据肿瘤的大小来判断它是不是恶性肿瘤。

首先，我们可以建立一个线性回归的模型 $h_\theta(X) = \theta^TX$。然后我们决定当 $h_\theta(X) >= 0.5$ 时认为是恶性肿瘤，反之则认为不是恶性。

但是这个模型是有问题的，当我们考虑更多的数据点时，线性回归模型可能就不再适用。例如，我们增加了几个数据后重新进行线性回归，依旧选定 0.5 作为分界线，这次，数据点 A 就被错误归类为“非恶性”。

课程里说，在这个例子中使用线性回归的一个问题是，线性回归的结果最终会小于 0 或超过 1，而在二分类任务里，本质上期望的值只有 0 和 1。线性模型的输出会随着输入的增大而增大，但数据的类别并不会随输入的增大而无限制增大。例如当 tumor size 不断增大时，线性回归的模型输入会最终大于 1，而实际上类别的取值不会超过 1，因此线性模型与分类问题是不相符的。

也因此，Sigmoid 函数的作用可以认为是对“线性回归”的一个改进，使得当输入无限增大时，模型的输出不会无限增大。最终的模型是一条曲线：

由于 sigmoid 函数的在 $-\infty$ 处几乎为 0，而 $\infty$ 处几乎为 1，因此在学习参数时两端的数据几乎不起作用。于是焦点就集中在两个类别的分界线，一个是 sigmoid 函数的位移，一个是倾斜程度，如图：

如果我们最终决策时只关心它的输出是大于还是小于 0.5，其实曲线的倾斜程度也没什么作用。

逻辑回归是线性模型？

首先我们来认识一下什么是决策边界。在二分类中，决策边界是数据集上的一个超平面，用来划分两个类别。例如上节的例子中，输入是一维 “tumor size”，因此决策边界是一个点，在线性回归模型或逻辑回归模型中，我们都可以认为是决策边界是 y 取 0.5 时对应的 “tumor size” 的值。

虽然 Sigmoid 函数是 S 形，但模型是不是“线性”并不是看输出结果的。从数学的角度看，逻辑回归的输出 $h_\theta(x) = sigmoid(\theta^Tx)$ 是全取决于输入 $x$ 的线性组合 $\theta^Tx$ ，因此逻辑回归是线性模型。我们再来直观感受一下，下面是输入是二维时逻辑回归的输出平面：

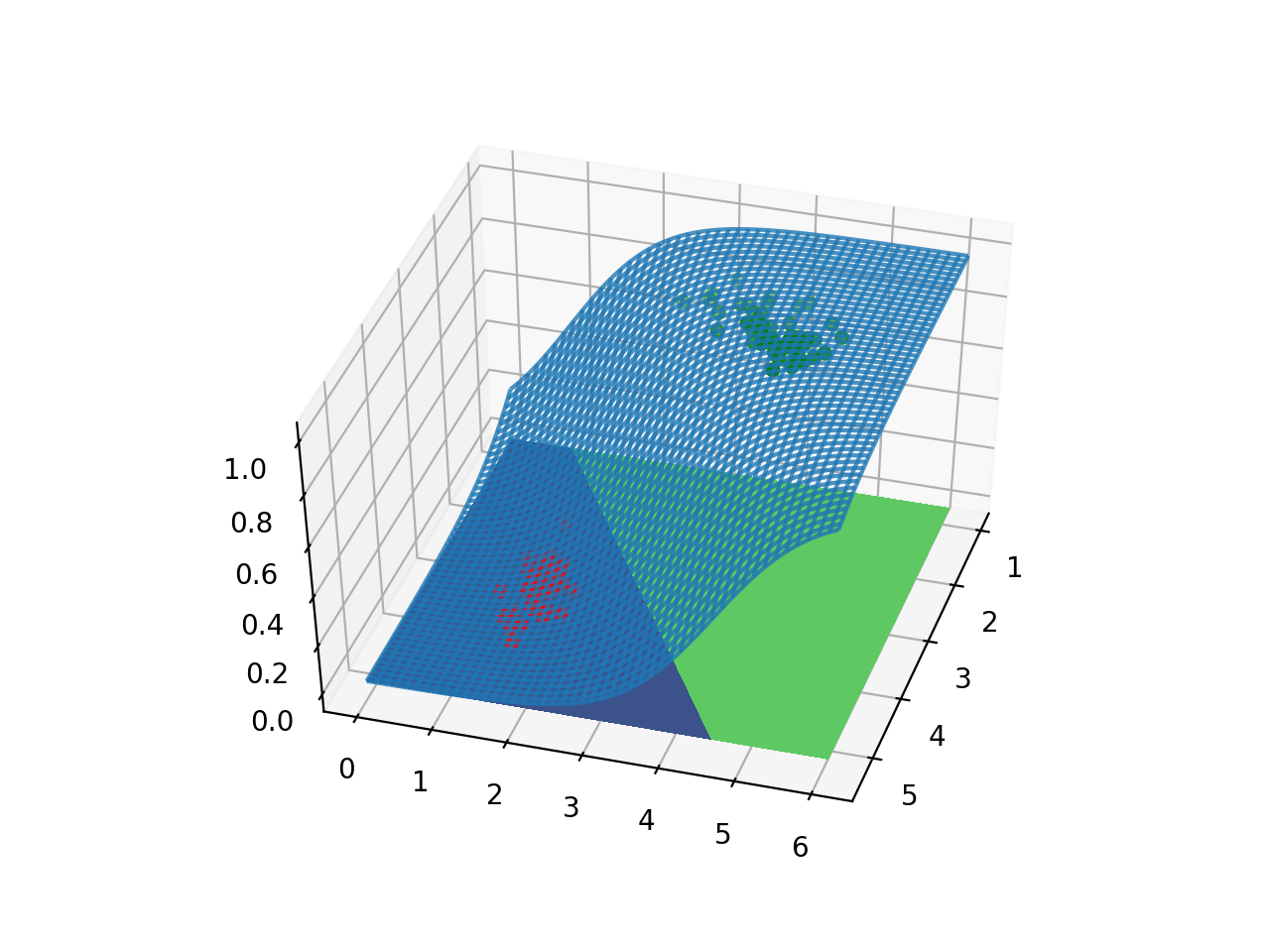
我们可以看到模型的输出是一个曲面。但模型的决策边界是模型输出为 0.5 时对应的输入。即上图中投影后的两个区域的边界。已经能看出这个边界是一条直线，我们将这个投影放在平面上：

要是有兴趣可以计算一下，它对应了 $\theta^Tx = sigmoid^{-1}(0.5)$ 这个平面。

如何实现非线性？

上面我们知道逻辑回归模型是线性模型，这意味着，如果样本的分布是非线性的，则采用逻辑回归的模型是没办法正确进行分类的，如下面这样的样本（数据取自 HanXiaoyang/ML-examples ）：

这时，模型本身的能力已经没办法提高了，于是我们需要从 输入 下手。我们观察数据的分布比较接近椭圆形，因此我们手工地多加入一些数据: $x_1^2, x_1x_2, x_2^2, x_1^3, x_1^2x_2, … x_2^6$。通过人工地加入更多的数据，我们赋予了逻辑回归拟合非线性数据的能力，下面是我们用这些数据进行的一次训练：

可以看到，两类数据被清楚地分开了，但由于引入过多的维数，也产生了过拟合的现象。这里要强调的是，逻辑回归如果要处理非线性的数据， 一定需要对输入进行预处理 。例如加入高次项，来引入非线性的能力。换句话说，还是要做“特征工程”。

损失函数

逻辑回归的 Hypothesis 为: $h_\theta(x) = 1 / (1 + e^{- \theta^T x})$，我们的任务是找到一个 “合适” 的 $\theta$ 来使这个 hypothesis 尽可能地解决我们的问题。例如分类任务，我们希望决策边界能最大程度将数据区分开。那么数学上怎么表达这种需求呢？

在线性回归中，一般采用均方误差用来评价一个 $\theta$ 的好坏：

$$ J(\theta) = \frac{1}{m}\sum_{i=1}^{m}{\frac{1}{2} (h_\theta(x^{(i)} ) - y^{(i)} )^2} $$

即 $J(\theta)$ 越小，认为 $\theta$ 越好。那为什么不直接把逻辑回归的 $h_\theta(x)$ 代入均方误差呢？原因是这样产生的 $J(\theta)$ 是非凸函数 (non-convex)。我们举个例子：

samples = [(-5, 1), (-20, 0), (-2, 1)]

def sigmoid(theta, x):
    return 1/(1 + math.e**(- theta*x))

def cost(theta):
    diffs = [(sigmoid(theta, x) - y) for x,y in samples]
    return sum(diff * diff for diff in diffs)/len(samples)/2

X = np.arange(-1, 1, 0.01)
Y = np.array([cost(theta) for theta in X])
plt.plot(X, Y)
plt.show()

可以看出这个损失函数是非凸的，局部最小值不等于全局最小值，因此使用梯度下降法难以求解。因此逻辑回归模型使用如下的损失函数，至于为它为什么是凸的，这里就不证明了：

$$ J(\theta) = \frac{1}{m}\sum_{i=1}^{m}{ Cost( h_\theta (x^{(i)}) , y)} \\ Cost( h_\theta (x) , y) = \begin{cases} -\log(h_\theta(x)), & \text{if}\ y = 1 \\ -\log(1 - h_\theta(x)), & \text{if}\ y = 0 \end{cases} $$

写成统一的形式：

$$ J(\theta) = - \frac{1}{m}\Big[\sum_{i=1}^{m}{ y^{(i)} \log h_{\theta} ( x^{(i)} ) + (1-y^{(i)} ) \log (1-h_\theta(x^{(i)} ) )}\Big] $$

那么损失函数是如何影响决策的呢？首先，损失函数是对 $h_\theta(x)$ 给出错误结论的惩罚。因此损失越小，一般就认为 $h_\theta(x)$ 的结论就越正确。而上面这个式子意味着，损失越小，最后得到的 $h_\theta(x)$ 曲面会越“贴近”数据点，换言之会“越陡”：

这幅图中，$J(\theta_{blue}) < J(\theta_{green})$，即蓝色曲面对应的 $\theta$ 的损失要小于绿色曲面对应的 $\theta$ 值。可以看到，损失小的蓝色曲面更陡。

损失函数对决策边界有何影响？我们取 $h_\theta(x) = 0.5$ 的决策边界，可以看到决策边界也有略微的不同：

但由于这两个 $\theta$ 都能把这两组数据区分开，因此它们并没有特别大的差别。这里博主猜想，逻辑回归的训练中，前几个迭代应该就能快速地制定出决策边界，接下来一些迭代的作用应该就是让 $h_\theta(x)$ “更陡”，一味追求损失更小究竟对决策边界有帮助吗？

小结一下，如何决定模型的损失函数？一是损失函数要正确评价参数，使损失更小的参数对解决问题更有利；另一方面，受限于优化手段，要求损失函数能求解。当然一些常用的模型损失函数也大致确定了。

正则化

如果出现过拟合，可以考虑去掉一些特征，但这些特征可能包含了重要信息，并不合适直接去掉。另一个方法就是加正则项。在逻辑回归中，加了正则项的损失函数如下：

$$ J(\theta) = - \frac{1}{m}\Big[\sum_{i=1}^{m}{ y^{(i)} \log h_{\theta} ( x^{(i)} ) + (1-y^{(i)} ) \log (1-h_\theta(x^{(i)} ) )}\Big] + \lambda \sum_{j=1}^{m}{( \theta_j^2 )} $$

注意公式最后增加的部分： $\lambda \sum_{j=1}^{m}{( \theta_j^2)}$ 就是所谓的“正则项”。它的存在意味着我们在优化时，不仅仅想让 $J(\theta)$ 尽可能小，同时也想保证 $\theta$ 也尽可能小。由此来减少过拟合。下面的图是我们取不同 $\lambda$ 时训练后的决策边界：

可以看到，随着 $\lambda$ 的增加，决策边界越来越平滑，但同时决策边界的准确性下降了。这是因为 $\lambda$ 过大时，优化 $J(\theta)$ 的主要目标变成了优化正则项而不是损失函数。

最后，我们看看这四个 $\lambda$ 的选择下，求得的 $\theta$ 的 $l_2$ 范数（即 $\theta$ 代表的向量的长度。

$\lambda$ norm of $\theta$
0 305.21
0.001 75.36
0.01 29.71
0.1 10.02

这也说明了如果我们增大正则项的比重，训练得到的 $\theta$ 会更小。而更小的 $\theta$ 通常意味着过拟合程度的减小，因为高次项所占的比重也会变小。

特征缩放

经常的，数据的各个特征的尺度不同，而如果差异很大，则会影响训练模型的速度。因此在训练前我们常常需要把各个特征缩放到同一尺度上。下图是用梯度下降法训练上节数据的学习曲线，可以看到差别相当明显。

偏置

在训练的时候，其实是需要手工加上偏置项 1 的，例如两维样本 $[x_1, x_2]$ 就需要扩充成 $[1, x_1, x_2]$，这个 1 就是所谓的偏置项。这样训练出来的 $\theta$ 就会比维度多一。偏置项有什么用呢？

让我们考虑一维数据，此时我们的 $h(x) = \theta \times x$，它代表了一条直线，且 必须过原点 。这样，如果样本偏离了原点，这条直线（决策边界）就没有办法很好地将数据分开。而加了偏置项，相当于模型变成 $h(x) = \theta_1 \times x + \theta_0$，就能表示任意的直线了。下面我们用 iris 数据分别训练了带偏置和不带偏置的两个模型：

我们看到，不带偏置 (bias) 的模型的决策边界过原点，因此没有办法将数据很好地划分开，而带偏置的模型则能很好地对数据进行划分。换句话说，偏置提供了平移的能力。

参考