f-divergence GAN 是对 GAN 框架的理论统一，本文学习过程中的一些笔记，包括基本公式的推导和重要概念的理解。

学习资料是李宏毅老师 关于 WGAN 的教学视频 视频里深入浅出地介绍了许多 GAN 的相关知识。不需要太多的数学基础就能听懂，强力推荐。

GAN 的基本思想

有这样一个 GAN 的应用，它能用机器生成 动漫头像。我们需要事先收集一些人类画师画的动漫头像，它们可以认为是图像空间(image page)里的某个分布 $P_{data}$。之后我们会尝试训练一个生成器 G，它能以随机噪声 $z$ 为输入，生成动漫头像，我们认为生成的头像满足分布 $P_G$。而训练的目标就是让 $P_G$ 尽可能地接近 $P_{data}$。换言之，我们希望机器生成的头像尽可能像人画出来的。

GAN Model (图片来源：https://blog.openai.com/generative-models/)

理论上，如果我们有完美的 loss 函数，则训练生成器 G 和普通的神经网络没有任何区别。很可惜，我们并没有办法真正求出 $P_{data}$ 和 $P_G$，也因此我们不可能找到一个完美的 loss 函数来衡量“$P_{data}$ 与 $P_G$ 是否接近”。于是 GAN 的想法是，我们再训练一个判别器(Discriminator) 来尽量近似这个完美的 loss 函数。GAN 的基本结构如下：

为了训练判别器 D，我们需要有正样本（动漫头像），也需要有负样本（非动漫头像）。正样本已经收集完毕，负样本哪里来呢？这就是 GAN 犀利的地方，它用生成器 G 生成的数据来作为负样本，用于训练判别器 D。而后我们得到一个更好的判别器 D 后，再用这个新的判别器 D 作为 loss 函数来训练 G 。于是我们能得到更好的生成器 G 以及判别器 D。

GAN 的算法

算法的伪代码如下：

  • 初始化 D, G 的参数 $\theta_d$ 和 $\theta_g$
  • 每一个迭代中：
    • 从真实数据的分布 $P_{data}(x)$ 中采样 $m$ 个样本 $\{x^1, x^2, \dots, x^m\}$
    • 从先验的噪声分布 $P_{prior}(z)$ 中采样 $m$ 个样本 $\{z^1, z^2, \dots, z^m\}$
    • 将噪声输入生成器 G，生成样本 $\{\tilde{x}^1, \tilde{x}^2, \dots, \tilde{x}^m\}, \tilde{x}^i = G(z^i)$
    • 更新判别器 D 的参数，即最大化：
      • $\tilde{V} = \frac{1}{m}\sum_{i=1}^m{\log D(x^i)} + \frac{1}{m}\sum_{i=1}^m{\log (1-D(\tilde{x}^i))}$
      • $\theta_d\leftarrow\theta_d+\eta\nabla\tilde{V}(\theta_d)$
    • 从先验的噪声分布 $P_{prior}(z)$ 中 再 采样 $m$ 个样本 $\{z^1, z^2, \dots, z^m\}$
    • 更新生成器 D 的参数，即最小化：
      • $\require{cancel}\tilde{V} = \cancel{\frac{1}{m}\sum_{i=1}^m\log D(x^i)} + \frac{1}{m}\sum_{i=1}^m\log (1-D(G(z^i)))$
      • $\theta_d\leftarrow\theta_d-\eta\nabla\tilde{V}(\theta_d)$

这里的疑问是，为什么要最大化 $\tilde{V}$ 呢？换成其它的 $\tilde{V}$ 行不行？其实 ƒ-divergence GAN 就是要告诉我们，这么设计 $\tilde{V}$ 是有道理的，并且换成其它的 ƒ-divergence 也没有问题。

ƒ-divergence

In probability theory, an ƒ-divergence is a function $D_f(P||Q)$ that measures the difference between two probability distributions $P$ and $Q$. It helps the intuition to think of the divergence as an average, weighted by the function f, of the odds ratio given by $P$ and $Q$.

给定两个分布 $P$ 和 $Q$，$p(x)$ 和 $q(x)$ 分别为对应样本的概率，ƒ-divergence 是一个这样的函数：

$$D_f(P||Q)=\int_xq(x)f(\frac{p(x)}{q(x)})dx$$

其中 $f$ 可以认为是 $D_f(P||Q)$ 的超参数，我们要求 $f$ 满足两点：(a) $f$ 是凸函数 (b) $f(1) = 0$

为什么 $D_f$ 可以衡量距离？

如果 $P = Q$，则 $D_f(P||Q) = 0$。证明很简单，我们知道 $f(1) = 0$，所以当 $p(x) = q(x)$ 时，有：

$$D_f(P||Q)=\int_xq(x)\underbrace{f(\overbrace{\frac{p(x)}{q(x)}}^{=1})}_{=0}dx=0$$

而如果 $P \neq Q$，有 $D_f(P||Q) > 0$。由于 $f$ 是凸函数，所以有：

$$ \require{cancel} \begin{eqnarray} D_f(P||Q) &=& \int_xq(x)f(\frac{p(x)}{q(x)})dx \\ &\ge& f(\int_x\cancel{q(x)}\frac{p(x)}{\cancel{q(x)}}dx)=f(1)=0 \end{eqnarray} $$

因此，我们可以用 ƒ-divergence 来衡量两个分布的距离，如果两个分布相同，则 ƒ -divergence 为 0，而若分布不同，则 ƒ-divergence 大于 0。

一些 ƒ-divergence

这里介绍的这些 divergence 我不知道是干什么用的。从应用的角度来说，似乎不明白也没什么关系。

当取 $f(x) = x \log x$ 时，我们就得到了 KL divergence：

$$D_f(P||Q)=\int_x q(x)\frac{p(x)}{q(x)}\log(\frac{p(x)}{q(x)})dx=\int_xp(x)\log(\frac{p(x)}{q(x)})dx$$

取 $f(x) = - \log x$ 时，我们就得到了 reverse KL-divergence:

$$D_f(P||Q)=\int_xq(x)(-\log(\frac{p(x)}{q(x)}))dx=\int_xq(x)\log(\frac{q(x)}{p(x)})dx$$

而取 $f(x) = (x-1)^2$ 时，得到的是 Chi Square divergence:

$$D_f(P||Q)=\int_x q(x)(\frac{p(x)}{q(x)}-1)^2dx = \int_x\frac{(p(x)-q(x))^2}{q(x)}dx$$

ƒ-divergence 不是距离

很重要的一点 f-divergence 不是“距离” (metric)，因为距离需要满足四个条件：

  1. $d(x, y) \ge 0$ 非负性
  2. $d(x, y) = 0$ 当且仅当 $x = y$
  3. $d(x, y) = d(y, x)$ 对称性
  4. $d(x, z) \le d(x, y) + d (y, z)$ 三角不等式

上面我们看到它满足前两个条件（严格来说 $D_f(P||Q) = 0$ 能不能推出 $P = Q$ 还不知道）。对剩下的条件，不同的 ƒ-divergence 有不同的情况。

例如 KL divergence 并不满足后对称性： $D_f(P||Q) \ne D_f(Q||P)$，也不满足三角不等式。证明我是肯定不会的，大家参考 维基百科 。

而 Jensen–Shannon (JS) Divergence就满足所有条件。一如既往，想看证明，请查看 原论文 。

Fenchel Conjugate

Conjugate 翻译是“共轭”，不明觉厉。对于每个凸函数，我们都可以 定义 一个它的共轭函数：

$$f^*(t) = \max_{x\in \mathbf{dom}(f)}\{xt-f(x)\}$$

对于理解 ƒ-divergence GAN 我们只需要知道对于常见常用的 $f$，我们可以定义并求出 $f^*$ 的表达式就行了。但尝试理解 $f^*$ 涵义对我们还是有帮助的。

我们看到，当 $x$ 取特定值 $x_0$ 时 $g(t) = x_0t - f(x_0)$ 是一条直线。我们取 $f(x) = x \log x$，x 取不同值时画出 $g(t)$ 的图像，如下所示：

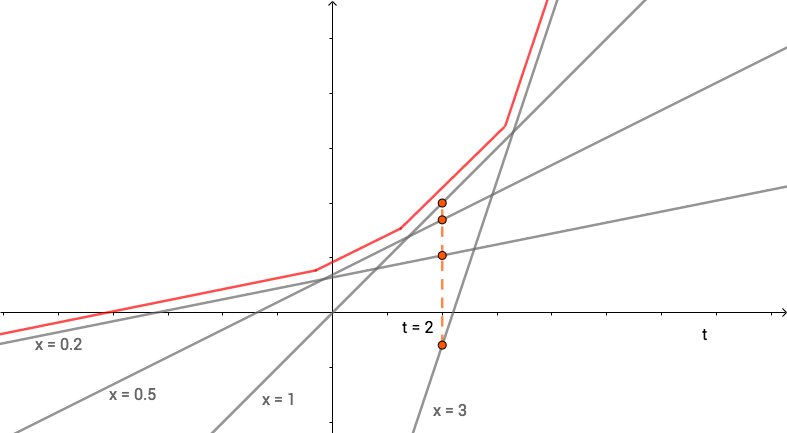
注意到 $f^*(t)$ 的定义为当 t 取某个值时，所有 $g(t)$ 的最大值。例如上图中，当 $t = 2$ 时，它与各直线的交点即为 $g(t)$ 的值，所以 $f^*(t)$ 的取值就是图点最高的点的值。

可以理解为，取不同的 x 值画出无穷多条直线 $g(t)$，这些直线的上边缘（上图红线）就是 $f^*(t)$。

最后，共轭函数有一个性质： $(f^* )^* = f$，也就是说：

$$f^*(t) = \max_{x\in \mathbf{dom}(f)}\{xt-f(x)\} \Longleftrightarrow f(x) = \max_{t\in \mathbf{dom}(f^*)} \{xt-f^*(x)\}$$

ƒ-divergence 与 GAN

我们知道，GAN 的目的是训练生成器 G，使其产生的数据分布 $P_G$ 与真实数据的分布 $P_{data}$ 尽可能小。换言之，如果我们用 ƒ-divergence 来表达 $P_G$ 与 $P_{data}$ 的差异，则希望最小化 $D_f(P_{data}||P_G)$。注意到：

\begin{eqnarray} D_f(P||Q) &=& \int_xq(x)f(\frac{p(x)}{q(x)})dx \\ &=& \int_xq(x)\left(\max_{t\in\mathbf{dom}(x^* )} \left\{\frac{p(x)}{q(x)}t-f^*(t)\right\}\right)dx \end{eqnarray}

于是乎，如果我们构造一个函数 $D(x) \in \mathbf{dom}(f^*)$，输入为 $x$，输出为 $t$，则我们可以把上式的 $t$ 用 $D(x)$ 替代。但由于函数 $D$ 输出的 $x$ 不一定能使 $f$ 最大，所以有：

\begin{eqnarray} D_f(P||Q) &\ge& \int_xq(x)\left(\frac{p(x)}{q(x)}D(x)-f^*(D(x))\right)dx \\ &=& \underbrace{\int_xq(x)D(x)dx - \int_xq(x)f^*(D(x))dx}_{M} \end{eqnarray}

因此，我们可以把求 $D_f(P||Q)$ 转化成一个最优化的问题：

\begin{eqnarray} D_f(P||Q) &\approx& \max_D\int_xp(x)D(x)dx-\int_xq(x)f^*(D(x))dx \\ &=& \max_D\left\{\underbrace{E_{x\sim P}[D(x)]}_{\text{Samples from P}} - \underbrace{E_{x\sim Q}[f^*(D(x))]}_{\text{Samples from Q}} \right\} \end{eqnarray}

上面做了这一系列的转换，归根结底是因为实际总是中，我们并没办法求出 $p(x)$ 或 $q(x)$，也没有办法穷举所有的 $x$，只能退而求其次求近似解。最终，我们把 GAN 的模型用数学公式表达即为：

$$ \begin{align} G^*&=\arg\min_GD_f(P_{data}||P_G) \\ &=\arg\min_G\max_D{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[f^*(D(x))]} \\ &= \arg\min_G\max_DV(G, D) \end{align} $$

当然，上面式子中的 $D$ 和我们在 GAN 模型里的判别器 D 还不一样。而且这个式子和我们之前说的 GAN 算法中的 $\tilde(V)$ 也是不同的。这是因为式子中的 $D$ 需要 $D(x) \in \mathbf{dom}(f^*)$。所以我们需要选择合适的 $D$ 才能满足上式。这里我就不推导了，大家有兴趣可以看 原文。

小结

ƒ-divergence GAN 是对 GAN 模型的统一，对任意满足条件的 $f$ 都可以构造一个对应的 GAN。

GAN 的目的是训练生成器 D 使之生成的数据对应的分布 $P_G$ 与真实数据的分布 $P_{data}$ 尽可能接近，即最小化 $D_f(P||Q)$。然而我们无法确切算出 $p(x)$ 及 $q(x)$，因此我们通过 Conjugate 将求 $D_f(P||Q)$ 转变成一个优化问题，于是我们的目标变成找到一个合适的函数 $D$ 来逼近 $D_f(P||Q)$。

参考