通过训练，我们可以从样本中学习到决策树，作为预测模型来预测其它样本。两个问题：

  1. 我们说要训练/学习，训练/学习什么？
  2. 为什么决策树可以用来预测？或者说它的泛化能力的来源是哪？

什么是决策树？

一棵“树”，目的和作用是“决策”。一般来说，每个节点上都保存了一个切分，输入数据通过切分继续访问子节点，直到叶子节点，就找到了目标，或者说“做出了决策”。这里我们举个喜闻乐见的例子吧。

现在有人给你介绍对象，你打听到对方的特点：白不白，富不富，美不美，然后决定去不去相亲。根据以往经验，我们给出所有可能性：

| 白   | 富   | 美   | 去   |
| 白   | 富   | 不美 | 去   |
| 白   | 不富 | 美   | 犹豫 |
| 白   | 不富 | 不美 | 犹豫 |
| 不白 | 富   | 美   | 去   |
| 不白 | 富   | 不美 | 去   |
| 不白 | 不富 | 美   | 犹豫 |
| 不白 | 不富 | 不美 | 不去 |

那么有人给我们介绍新的对象的时候，我们就要一个个特点去判断，于是这种判断的过程就可以画成一棵树，例如根据特点依次判断：

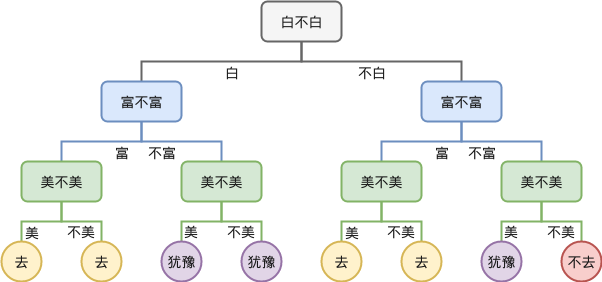
这就是决策树，每一层我们都提出一个问题，根据问题的回答来走向不同的子树，最终到达叶子节点时，做出决策（去还是不去）。可以看到，决策树没有任何特别的地方。

当然，如果我们先考虑富不富，再考虑白不白，则得到的树又不相同：

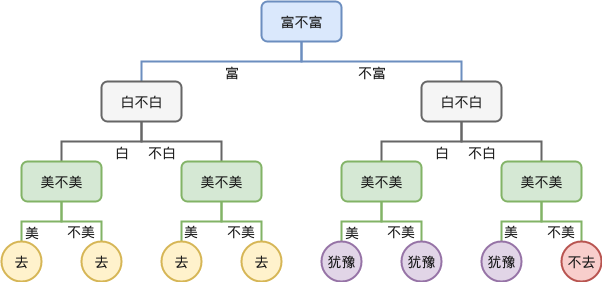
所以，决策树其实就是根据已知的经验来构建一棵树。可以认为是根据数据的某个维度进行切分，不断重复这个过程。当然，如果切分的顺序不同，会得到不同的树。

既然如此，按不同顺序切分得到的决策树又有什么不同呢？

训练，训练什么？

如果仔细观察，我们发现决策树中有一些叶子节点是可以合并的，合并之后，到达某个节点时就不需要进行额外的决策，例如切分顺序“白，富，美”得到的决策树合并后如下：

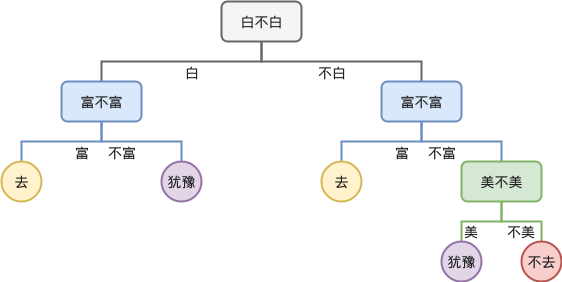
我们先记着，合并后的树有 5 个叶子节点。

而“富，白，美”的决策树合并后变成：

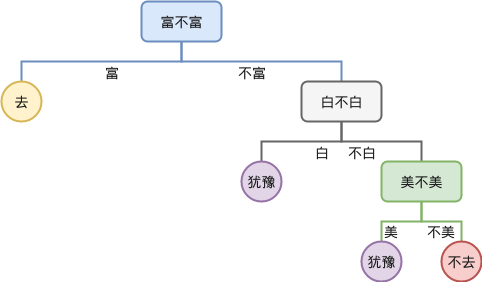
可以看到上面这棵树则只有 4 个叶子节点，少于“白，富，美”的 5 个节点。

这就是决策树间最大的区别，不同决策树合并后得到树叶子节点的个数是不同的，后面我们会看到，叶子节点越少，往往决策树的泛化能力越高，所以可以认为训练决策树的一个目标是 减少决策树的叶子节点 。这个任务其实是很困难的，考虑数据有 n 维，那么切分的顺序的可能性就是n!。因此实际中一般并不是求全局最优，而是采用贪心算法求局部最优。

另外，节点在什么时候才能合并呢？一般需要叶子节点的标签/决策相同。也因此，后面提到贪心的指标时，往往指标的目的就是选择某一个维度，使得划分后的子集合更 有序。

（当然上面的说法不准确，决策树就是一棵树，建成什么样子其实全凭心情/需求。在搜索过程中其实并找不到官方的优化目标，上面的结论是博主自己得出的，而它能帮助我们理解下一个问题：决策树为什么有泛化能力？）

泛化能力

细心的读者会发现，决策树好像根本没什么用？

在上面的例子里，我们只需要记住切分的顺序，例如“富，白美”，然后在原数据中一个个匹配就行了，树的结构虽然方便理解，但它也没有存在的必要。而这个疑问的一个引申，既然我们能通过查表来做决策，但之前又说决策树可以用来做预测，那么决策树的泛化能力（即“预测”能力）来自哪里呢？

节点的合并是泛化能力的根本

上面的例子中我们有三个维度，每个维度有两种可能，并且我们的经验已经覆盖了所有的 8 种情况。但实际生活中我们的样本不可能覆盖所有的可能性，因此在我们合并节点的过程中就悄悄地覆盖了一些未知的数据。例如我们只遇到过 4 种情况（这里的决策和上面的例子不同）：

| 白   | 富   | 美   | 去   |
| 白   | 不富 | 美   | 犹豫 |
| 不白 | 不富 | 美   | 犹豫 |
| 不白 | 不富 | 不美 | 不去 |

在此基础上构建决策树（顺序为富，白，美）：

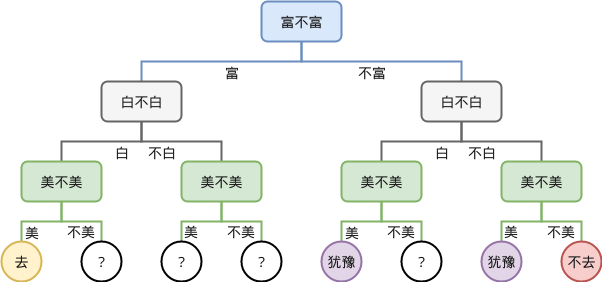
于是在合并的过程中，我们把没有见过数据都忽略，于是合并后的树为：

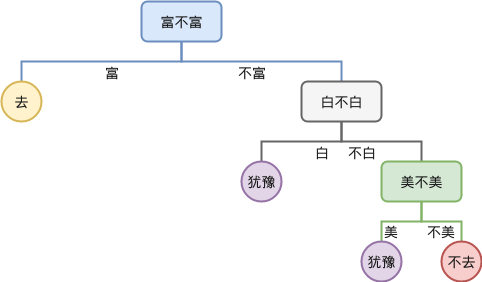
对于这棵决策树，如果遇到新的数据 白，富，不美 我们也可以推测值得 去，或者对于 白，不富，不美 我们就会 犹豫。

当然，我们的示例自下向上合并，是为了方便展示，实际构建决策树时，如果某个分支只有一个样本，会直接停止展开。如，在“富”的分支上，我们只见到一个样本，结果是“去”，因此会停止继续向下展开。这和算法中的剪枝是相同的想法。

类别的切分也能提供泛化能力

上面的例子里我们的数据都是“类别型”，即一个维度/特征的取值是离散的，例如“富”，只能取两个值“富”和“不富”。但实际生活中，一个维度的取值可以是连续的，例如人的身高，体重，工资等。

那么，当决策树的一个节点需要切分时，我们不可能穷举所有的可能，因此需要做一定的取舍。常见的作法是对数据做一个“二切分”。例如我们知道三个人的身高： 153, 164, 182，我们切分成 <= 164 和 > 164 两类（也可以用其它的切分方法）。

这种 模糊的切分 也提供了泛化能力。例如一个新的数据，身高 175，我们自然就能归到 > 164 的切分中，即使之前根本没见过这个数据。

贪心指标

一般我们是用贪心算法来构建决策树，这就引申出了一些常用的指标，帮助我们决定在每次切分时，选择哪个维度进行切分；遇到数值类型需要做二切分时，具体用哪个数值。下面我们介绍两个常用的指标：

基尼不纯度 Gini impurity

一个集合有 $J$ 个类别，我们记 $i \in { 1, 2, …, J }$，且 $p_i$ 表示该集合中标记为类别 $i$ 的元素所占的比例，则 基尼不纯度 定义为：

$$ I_{G}( p ) = \sum_{i=1}^J p_i \sum_{k\neq i} p_k = \sum_{i=1}^{J} p_i (1-p_i) = \sum_{i=1}^{J} (p_i - {p_i}^2) = \sum_{i=1}^J p_i - \sum_{i=1}^{J} {p_i}^2 = 1 - \sum^{J}_{i=1} {p_i}^{2} $$

想象我们有一堆乒乓球，和一堆标签，为每个球上贴一个标签，这组成了我们的原始样本。现在，我们再买和之前一样的一堆标签，为每个球上再贴一个标签。那么现在球上有两个标签，它们可能一样，也可能不一样。基尼不纯度指的就是贴了不同标签的球的占比。一个很直观的结论是，如果集合里的标签都一样，那么基尼不纯度就为 0。

所以在数学上，我们可以先考虑标签 $i$，一个球上第一个标签贴为 $j$ 的概率记为 $p_i$，那么贴第二个标签时，要求贴的是非 $i$ 的标签，因此概率是 $\sum_{k \ne i}{p_k} = 1 - p_i$。那么贴了不同标签的球所占的比例就是 $\sum_{i=1}^J p_i \sum_{k\neq i} p_k$。

上面提到，决定用哪个维度进行切分时，一个标准是使切分后的子集更 有序，这里也意味着基尼不纯度更小。于是我们选择某一个维度进行切分，求得所有子集的基尼不纯度之和。总有一个维度使得这个和取到最小，对应的维度就是当前最佳的切分维度。当然，维度确定后，对于数值型的维度，其实还要确认具体的切分点，也可以用基尼不纯度来作为切分的依据。

信息熵增益 Information Gain

首先要了解的是 信息熵 在有限样本时定义为：

$$ H(X) = \sum_{i}{P(x_i)I(x_i)} = -\sum_i{P(x_i)\log_2{P(x_i)}} $$

$-\log_2{P(x_i)}$ 的大意是一个事件 $x_i$ 如果出现的概率越小，那么当它发生时我们就越吃惊，代表的就是一个事件“吃惊程度”。而熵就是所有事件的“吃惊程度”的期望值。一般地，如果一个集合的熵越大，则集合越无序；熵越小，则集合越有序。换句话说，如果熵越大，说明我们越容易吃惊，说明集合无序，我们很难预测下一个出现的是什么，相反，熵越小，说明我们越容易猜测集合里有什么，说明集合越有序。

而在决策树的切分里，事件 $x_i$ 可以认为是在样本中出现某个标签/决策。于是 $P(x_i)$可以用所有样本中某个标签出现的频率来代替。

但我们求熵是为了决定采用哪一个维度进行切分，因此有一个新的概念 条件熵：

$$ H(X|Y) = \sum_{y \in Y}{p(y) H(X|Y=y)} $$

这里我们认为 $Y$ 就是用某个维度进行切分，那么 $y$ 就是切成的某个子集合于是 $H(X|Y=y)$ 就是这个子集的熵。因此可以认为就条件熵是每个子集合的熵的一个加权平均/期望。最后，如何判断一个维度更优秀呢？我们采用信息熵增益：

$$Gain(Y) = H(X) - H(X|Y)$$

即切分后，Gain 最高的那个维度，我们优先用它来切分子集。

决策树的实现

这里用 python 来实现一下基本的决策树（非数值型），再用上面的例子实验实验。完整代码请见 gist 。

首先决定输入的结构：

data = [['白',   '富',   '美',   '去'],
        ['白',   '富',   '不美', '去'],
        ['白',   '不富', '美',   '犹豫'],
        ['白',   '不富', '不美', '犹豫'],
        ['不白', '富',   '美',   '去'],
        ['不白', '富',   '不美', '去'],
        ['不白', '不富', '美',   '犹豫'],
        ['不白', '不富', '不美', '不去']]

数据是一个 List，每一个元素也是一个 List，代表样本的多个维度，最后一维存放标签。

下面先实现一个切分的函数，作用是将一系列样本，根据某个维度，切分到不同的集合。

def _split_samples(self, samples, feature):
    """Split samples into subsets, according to the feature

    :samples: List[List[val]]
    :feature: Int
    :returns: {val: List[data]} a dict contains the data of subsets

    """
    ret = {}
    for sample in samples:
        val = sample[feature]
        ret.setdefault(val, [])
        ret[val].append(sample)
    return ret

有了切分的函数我们就能创建决策树了，下面这个函数是递归调用，给定一些数据，如果 _stop_now 判断已经不需要继续切分了，则返回这些数据的标签（一般来说这些数据的标签会相同），否则我们调用 _get_feature 来决定用哪个维度进行切分，并对每个子集合调用递归调用 _split 创建节点。

树的节点我们用 dict 表示，例如 {'白': ..., '不白', ...}。

def _split(self, data, level=0):
    """recursively split the data for node

    :data: List[data]
    :returns: label if should stop, else a node of the tree

    """

    if self._stop_now(data):
        return data[0][-1]

    # split the data
    feature = self._get_feature(data, level)
    subsets = self._split_samples(data, feature)

    return {key: self._split(subset, level+1) for key, subset in subsets.items()}

接下来，我们只需要实现 _stop_now 和 _get_feature 就可以了。对于 _stop_now，我们认为如果所有样本都是同一个标签就可以停止：

def _stop_now(self, data):
    """check if we need to stop now

    :data: List[data]
    :returns: Boolean

    """
    labels = [d[-1] for d in data]
    return len(set(labels)) <= 1

而 _get_feature，我们按输入的维度顺序切分，因此实现是：

def _get_feature(self, data, level):
    """Decide which feature to be used to split data

    :data: List[data]
    :level: Int the level of the tree
    :returns: Int the dimension of the data to be used for split data

    """
    return level

最后把上面这些代码放到一个类里：

class DecisionTree(object):
    def __init__(self, data):
        """Learn a decision tree from data and label

        :data: List[List[val]], a list contains M sample, each sample is represented by a List
               The last column of the sample is the label
        :returns: The root of a decision tree

        """

        super(DecisionTree, self).__init__()
        self.root = self._split(data)

    # rest of the methods

tree = DecisionTree(data)
print(tree.root)

得到的结果是：

{
    '白': {
        '富': '去',
        '不富': '犹豫'
    },
    '不白': {
        '富': '去',
        '不富': {
            '美': '犹豫',
            '不美': '不去'
        }
    }
}

可以看到，和我们前面手工合并的结果是一样的。

熵增益

下面我们实现信息熵增益指标，首先是熵的计算

import math
def _entropy(self, dataset):
    """calculate the entropy of a dataset

    :dataset: List[data], each data is List[val], last column is label
    :returns: Float

    """
    counts = {}
    for data in dataset:
        label = data[-1]
        counts.setdefault(label, 0)
        counts[label] += 1

    total_num = len(dataset)
    return sum([-count/total_num * math.log2(count/total_num) for count in counts.values()])

然后是条件熵的计算：

def _conditional_entropy(self, dataset, feature):
    """calculate the conditional entropy of dataset on feature

    :dataset: List[data]
    :feature: Int
    :returns: Float

    """
    subsets = self._split_samples(dataset, feature)
    total_num = len(subsets)
    return sum([len(subset)/total_num * self._entropy(subset) for subset in subsets.values()])

最后，替换之前的 _get_feature，也就是在决定用什么维度进行切分时，我们选择熵增益最大的维度：

def _get_feature(self, data, level):
    dimensions = len(data[0]) - 1
    entropy = self._entropy(data)

    gains = [entropy - self._conditional_entropy(data, i) for i in range(dimensions)]
    return gains.index(max(gains))

我们再用这个策略去“训练”前面的数据，得到的结果为：

{
    '富': '去',
    '不富': {
        '白': '犹豫',
        '不白': {
            '美': '犹豫',
            '不美': '不去'
        }
    }
}

可以看到，结果对应了“富，白，美”的切分顺序。而之前我们也知道，这个顺序有 4 个叶子节点，而默认切分 “白，富，美” 有 5 个叶子节点。也证明这样的优化目标是有效的。

小结

“训练”决策树是为了减少决策树最后的叶子节点，由于训练全局最优很困难，因此人们用一些局部的贪心策略进行训练，例如上文介绍的信息熵增益。

决策树的泛化能力主要来源于叶节点的合并。因此，如果决策树“过拟合”，其实意味着合并的节点不够多。

最后，本文代码的完整版请见 Gist: decision tree

参考