Michael Nielsen 的 深度学习 文章里对 BP 算法有了相当全面的介绍，网上也有中文翻译版本。本文是自己学习的一些笔记，主要是抄一遍公式的证明来加强记忆。

符号说明

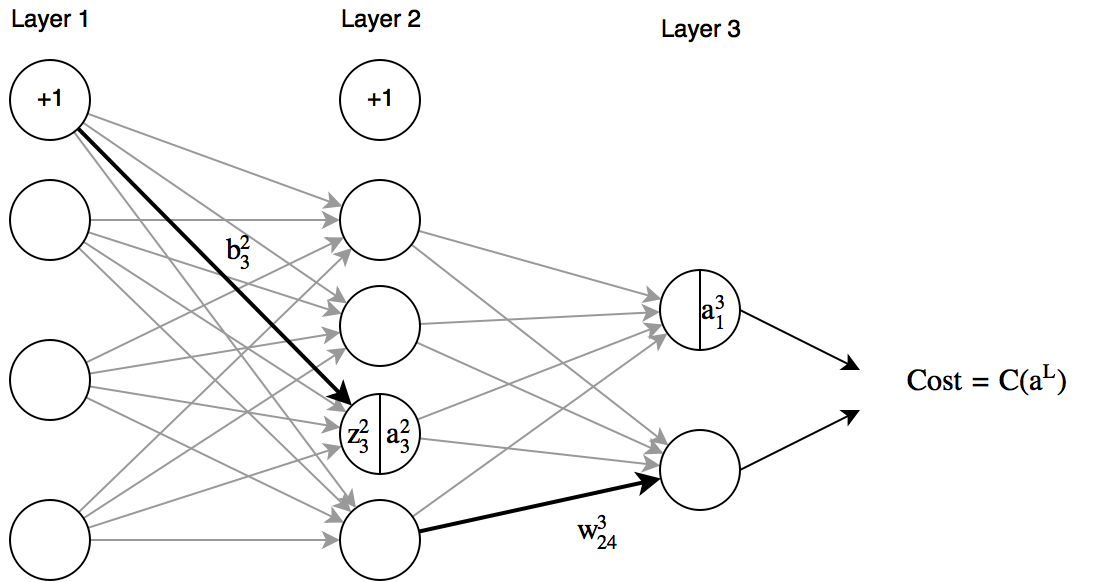
  • $b_j^l$ 表示第 $l$ 层的第 $j$ 个节点对应的偏置
  • $w_{jk}^l$ 表示从第 $l-1$ 层的第 $k$ 个节点到 $l$ 层的 $j$ 个节点的连线的权重。
  • $z_j^l$ 表示第 $l$ 层的第 $j$ 个节点的加权输入，即 $z_j^l \equiv \sum_k{w_{kj}^l a_k^{l-1}} + b_j^l$
  • $a_j^l$ 表示第 $l$ 层的第 $j$ 个节点的激活输出，即 $a_j^l \equiv \sigma(z_j^l)$

BP 算法

  1. 输入 $x$: 设输入层的激活值 $a^1 = x$。
  2. 前向传播：对于 $l = 2, 3, …, L$，计算 $z^l = w^l a^{l-1} + b^l$ 及 $a^l = \sigma(z^l)$。
  3. 计算 error $\delta^L = \nabla_a C \odot \sigma’(z^L)$。
  4. 反射传播错误：对于 $l = L-1, L-2, …, 2$ 计算 $\delta^l = (( w^{l+1} )^T \delta^{l+1} ) \odot \sigma’(z^l)$
  5. 输出每层的梯度变化： $\nabla_{w^l} C = \delta^l (a^{l-1} )^T $ ， $\nabla_{b^l} C = \delta^l$

如果算法需要计算多个样本 $x$ 对应的梯度变化，然后取平均时，可以输入 $X = [x_1, x_2, …, x_m]$，其中 $m$ 为样本数目。上面的算法不需要任何的修改，算法的输入变为：$\nabla_{b^l} C = [\nabla_{b^{l, 1}} C, \nabla_{b^{l, 2}} C, … \nabla_{b^{l, m}} C]$ ，$\nabla_{w^l} C = \sum_m{w^{l, m}}$ ，其中上标 ${l, m}$ 代表第 $m$ 个样本对应的第 $l$ 层。这可以认为是算法在多个样本下的矩阵形式。

四个基本公式

矩阵形式：

\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma’(z^L). \tag{BP1a}\end{eqnarray}

\begin{eqnarray} \delta^l = (( w^{l+1} )^T \delta^{l+1} ) \odot \sigma’(z^l ) \tag{BP2a}\end{eqnarray}

\begin{eqnarray} \nabla_{b^l} C = \delta^l \tag{BP3a}\end{eqnarray}

\begin{eqnarray} \nabla_{w^l} C = \delta^l (a^{l-1} )^T \tag{BP4a}\end{eqnarray}

分量形式：

\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma’(z^L_j) \tag{BP1}\end{eqnarray}

\begin{eqnarray} \delta^l_j = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma’(z^l_j). \tag{BP2}\end{eqnarray}

\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j \tag{BP3}\end{eqnarray}

\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j. \tag{BP4}\end{eqnarray}

公式推导

这里涉及很多变量和下标，这是理解神经网络“最大”的门槛了吧。下面我们要证明上面提到的四个公式，证明的过程基本是原文的翻译。

BP1

下面我们先证明公式 BP1，我们要先定义 $\delta_j^l$：

$$\delta^l_j \equiv \frac{\partial C}{\partial z^l_j}$$

根据链式法则，由于 $C$ 是 $a_1^L, a_2^L, …$ 的函数，所以有

$$\delta^L_j = \sum_k{\frac{\partial C}{\partial a_k^L} \frac{\partial a_k^L}{\partial z_j^L}}$$

其中 $k$ 是输出层 L 的节点个数。当然，根据 $a_j^l$ 的定义我们知道，$a_j^l$ 完全取决于 $z_j^l$ 的值。这意味着当 $j \ne k$ 时，$\partial a_k^L/\partial z_j^L = 0$。于是上式又可以简化成：

$$\delta^L_j = \frac{\partial C}{\partial a_j^L} \frac{\partial a_j^L}{\partial z_j^L}$$

而由于 $a_j^L = \sigma(z_j^L)$，上式的第二项就可以用 $\sigma’(z_j^L)$ 替换，于是得到公式 BP1 ：

\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma’(z^L_j) \tag{BP1}\end{eqnarray}

上式中 $\frac{\partial C}{\partial a_j^L}$ 取决于损失函数 $C$ 的选择，当 $C = \frac{1}{2}\sum_j(y_j - a_j^L )^2$ 时，有 $\partial C/\partial a_j^L = (a_j^L - y_j)$。

矩阵形式如下：

\begin{eqnarray} \delta^l = \begin{bmatrix} \delta_1^L \\ \delta_2^L \\ \vdots \\ \delta_j^L \end{bmatrix} = \begin{bmatrix} \frac{\partial C}{\partial a_1^L} \\ \frac{\partial C}{\partial a_2^L} \\ \vdots \\ \frac{\partial C}{\partial a_j^L} \end{bmatrix} \odot \begin{bmatrix} \sigma’(z_1^L) \\ \sigma’(z_2^L) \\ \vdots \\ \sigma’(z_j^L) \end{bmatrix} = \nabla_a C \odot \sigma’(z^L) \tag{BP1a}\end{eqnarray}

BP2

类似的，我们从定义出发：

$$ \delta_j^l = \frac{\partial C}{\partial z_j^l} $$

类似上一节，$C$ 可以认为是任意一层的所有参数 $z_1^l, z_2^l, …$ 的复合函数，因此根据链式法则：

$$ \delta_j^l = \frac{\partial C}{\partial z_j^l} = \sum_k{\frac{\partial C}{\partial z_k^{l+1}} \frac{\partial z_k^{l+1}}{\partial z_j^l}} = \sum_k{\delta_k^{l+1} \frac{\partial z_k^{l+1}}{\partial z_j^l}} $$

根据 $z_k^{l+1}$ 的定义，我们又有：

$$ z_k^{l+1} = \sum_j{w_{kj}^{l+1} a_j^l + b_k^{l+1 }} = \sum_j{w_{kj}^{l+1} \sigma(z_j^l )+b_k^{l+1}} $$

对 $z_j^l$ 求导，注意到只有当 $z_j$ 匹配时导数才不为零，所以有 ：

$$\frac{\partial z_k^{l+1}}{\partial z_j^l} = w_{kj}^{l+1}\sigma’ (z_j^l)$$

最后代入 $\delta_j^l$ 的式子，即为公式 BP2：

\begin{eqnarray} \delta^l_j = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma’(z^l_j). \tag{BP2}\end{eqnarray}

矩阵形式如下：

\begin{eqnarray} \delta^l &=& \begin{bmatrix} \delta_1^l \\ \delta_2^l \\ \vdots \\ \delta_j^l \end{bmatrix} = \begin{bmatrix} w_{11}^{l+1} & w_{21}^{l+1} & \dots & w_{k1}^{l+1} \\ w_{12}^{l+1} & w_{22}^{l+1} & \dots & w_{k2}^{l+1} \\ \dots & \dots & \dots & \dots \\ w_{1j}^{l+1} & w_{2j}^{l+1} & \dots & w_{kj}^{l+1} \end{bmatrix} \begin{bmatrix} \delta_1^{l+1} \\ \delta_2^{l+1} \\ \vdots \\ \delta_k^{l+1} \\ \end{bmatrix} \odot \begin{bmatrix} \sigma’(z_1^L) \\ \sigma’(z_2^L) \\ \vdots \\ \sigma’(z_j^L) \end{bmatrix} \\ &=& (( w^{l+1} )^T \delta^{l+1} ) \odot \sigma’(z^l ) \tag{BP2a}\end{eqnarray}

BP3

由于 $b_j^l$ 的作用于 $z_j^l$ 的作用基本一致，所以对于 BP2 的证明几乎可以直接对 $b_j^l$ 使用。$C$ 可以认为是任意一层的所有参数 $z_1^l, z_2^l, …$ 的复合函数，因此根据链式法则：

$$ \frac{\partial C}{\partial b_j^l} = \sum_k{\frac{\partial C}{\partial z_k^{l+1}} \frac{\partial z_k^{l+1}}{\partial b_j^l}} = \sum_k{\delta_k^{l+1} \frac{\partial z_k^{l+1}}{\partial b_j^l}} $$

根据 $z_k^{l+1}$ 的定义，我们又有：

$$ z_k^{l+1} = \sum_j{w_{kj}^{l+1} a_j^l + b_k^{l+1 }} = \sum_j{w_{kj}^{l+1} \sigma(z_j^l )+b_k^{l+1}} $$

对 $b_j^l$ 求导，注意到只有当 $z_j$ 匹配时导数才不为零，所以有 ：

$$ \frac{\partial z_k^{l+1}}{\partial b_j^l} = w_{kj}^{l+1} \frac{\partial \sigma (z_j^l )}{\partial z_j^l} \frac{\partial z_j^l }{\partial b_j^l } = w_{kj}^{l+1}\sigma’ (z_j^l) $$

代入公式，有：

\begin{eqnarray} \frac{\partial C}{\partial b_j^l} = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma’(z^l_j) = \delta^l_j \tag{BP3}\end{eqnarray}

矩阵形式如下：

\begin{eqnarray} \nabla_{b^l} C = \delta \tag{BP3a}\end{eqnarray}

BP4

证明过程中先运用链式法则引入 $z_j^l$，之后代入 $z_j^l = \sum_k{w_{kj}^l a_k^{l-1}} + b_j^l$ 求导即可。

\begin{eqnarray} \frac{\partial C}{\partial w_{kj}^l} &=& \sum_i{\frac{\partial C}{\partial z_i^l} \frac{\partial z_i^l}{\partial w_{kj}^l}} \\ &=& \frac{\partial C}{\partial z_j^l} \frac{\partial z_j^l}{\partial w_{kj}^l} = \delta_j^l \frac{\partial z_j^l}{\partial w_{kj}^l} \\ &=& \delta_j^l \Big( \sum_i{\frac{\partial w_{ij}^l a_i^{l-1}}{\partial w_{kj}^l}} + \frac{\partial b_j^l}{\partial w_{kj}^l} \Big) \\ &=& \delta_j^l a_k^{l-1} = a_k^{l-1} \delta_j^l \tag{BP4}\end{eqnarray}

矩阵形式如下（为了方便观看，把 $\partial C/\partial w_{kj}^l$ 与成了 $w_{kj}^l$）：

\begin{eqnarray} \nabla_{w^l} C = \begin{bmatrix} w_1^l \\ w_2^l \\ \dots \\ w_j^l \end{bmatrix} &=& \begin{bmatrix} w_{11}^l & w_{21}^l & \dots & w_{k1}^l \\ w_{12}^l & w_{22}^l & \dots & w_{k2}^l \\ \dots & \dots & \dots & \dots \\ w_{1j}^l & w_{2j}^l & \dots & w_{kj}^l \end{bmatrix} \\ &=& \begin{bmatrix} a_1^{l-1} \delta_1^l & a_2^{l-1} \delta_1^l & \dots & a_k^{l-1} \delta_1^l \\ a_1^{l-1} \delta_2^l & a_2^{l-1} \delta_2^l & \dots & a_k^{l-1} \delta_2^l \\ \dots & \dots & \dots & \dots \\ a_1^{l-1} \delta_j^l & a_2^{l-1} \delta_j^l & \dots & a_k^{l-1} \delta_j^l \end{bmatrix} \\ &=& \begin{bmatrix} \delta_1^{l} \\ \delta_2^{l} \\ \vdots \\ \delta_j^{l} \end{bmatrix} \begin{bmatrix} a_1^{l-1} & a_2^{l-1} & \dots & a_k^{l-1} \end{bmatrix} \\ &=& \delta^l (a^{l-1} )^T \tag{BP4a}\end{eqnarray}

代码实现

可以在 lotabout/neural-network.py 中找到，代码在原文的基础之上实现了 mini batch 的矩阵运算。

参考资料